Kinematics - Rigid Body Transformation

Rigid Body Transformations

Notations

• $R_{C}^A$ represents the orientation of frame $C$ with respect to frame $A$.
• $T_{C}^A$ represents the translation of frame $C$ with respect to frame $A$.
• $H_{C}^A$ represents the homogeneous transformations of frame $C$ with respect to frame $A$.

$$H_{C}^A = \begin{bmatrix} R_{C}^A & T_{C}^A \\ 0 & 1 \end{bmatrix}$$

Where, in 3d, $R_{C}^A$ is a 3 $\times$ 3 matrix, $T_{C}^A$ is a $3\times 1$ vector.

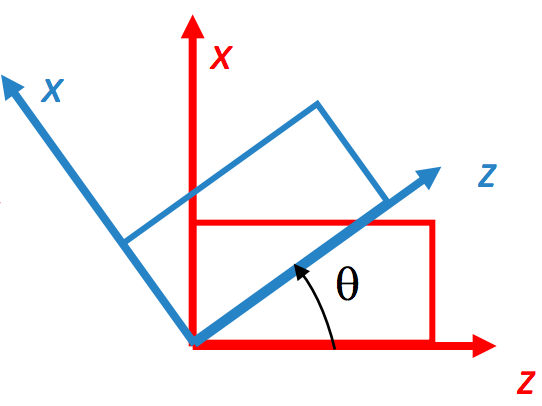
• $R_{x,\phi},R_{y,\theta}, R_{z, \psi}$ represent rotations about the axis (right-hand rule) by angle

$$R_{x,\phi} = \begin{bmatrix} 1 & 0 & 0 \\ 0 & cos(\phi) & -sin(\phi) \\ 0 & sin(\phi) & cos(\phi) \end{bmatrix}, R_{y,\theta} = \begin{bmatrix} cos(\theta) & 0 & sin(\theta) \\ 0 & 1 & 0 \\ -sin(\theta) & 0 & cos(\theta) \end{bmatrix}, R_{z,\psi} = \begin{bmatrix} cos(\psi) & -sin(\psi) & 0 \\ sin(\psi) & cos(\psi) & 0 \\ 0 & 0 & 1 \end{bmatrix}$$

Composite Transformations

• Post-multiply successive transformations about intermediate frames

$$R_{2}^0 = R_{1}^0 R_{2}^1$$

• Pre-multiply successive transformations about fixed frames

$$R_{2}^0 = R_{2}^1 R_{1}^0$$

Composition of homogeneous transformations follows the rules of rotation matrices.

Inverse Transformations

• Rotations

$$R^{-1} = R^T$$

• Homogeneous transformations

$$H = \begin{bmatrix} R & T \\ 0 & 1 \end{bmatrix} \\ H^{-1} = \begin{bmatrix} R^T & -R^TT \\ 0 & 1 \end{bmatrix} \neq H^T$$

Skew Symmetric Matrices

$$\bf{a}\times \bf{b} = \begin{bmatrix} a_1 \\ a_2 \\ a_3 \end{bmatrix} \times \begin{bmatrix} b_1 \\ b_2 \\ b_3 \end{bmatrix} = \begin{bmatrix} a_2b_3 - a_3b_2 \\ a_3b_1 - a_1b_3 \\ a_1b_2 - a_2b_1 \end{bmatrix} = \begin{bmatrix} 0 & -a_3 & a_2 \\ a_3 & 0 & -a_1 \\ -a_2 & a_1 & 0 \end{bmatrix} \begin{bmatrix} b_1 \\ b_2 \\ b_3 \end{bmatrix} = \hat{\bf{a}} \bf{b} \\ $$

$\hat{\bf{a}} = \begin{bmatrix} 0 & -a_3 & a_2 \\ a_3 & 0 & -a_1 \\ -a_2 & a_1 & 0 \end{bmatrix}$ is the skew symmetrix matrix.

For any skew symmetrix matrix $A^T = -A$.

2D Rotation

$$R = \begin{bmatrix} cos(\theta) & -sin(\theta)\\ sin(\theta) & cos(\theta) \end{bmatrix}$$

The rotation in 2d can be viewed as the complex number $Z(\theta) = cos(\theta) +i sin(\theta)$

$$(cos(\theta) + isin(\theta)) (x + iy) = (xcos(\theta) - ysin(\theta))+ (xsin(\theta) +ycos(\theta))i \\ = (xcos(\theta) - ysin(\theta), xsin(\theta) +ycos(\theta)) = R \begin{bmatrix} x\\ y \end{bmatrix}$$

Rodrigues’ Formula

Rodrigues’ formula gives us an decomposition of the rotation matrix into axis and angle.

$$R_{r,\theta} = I cos(\theta) + rr^T(1-cos(\theta)) + \hat{r} sin(\theta) \\ cos(\theta) = \frac{(trR) - 1}{2}\\ \hat{r} = \frac{\theta}{2sin(\theta)} (R-R^T)$$

Quaternions

Quatornion is a 4 dimensional representation of the rotation matrix. The basis are $\{1, i, j, k\}$. The quatornion is a generalization of complex number.

$$ij = k, jk = i, ki = j, i^2 = j^2 =k^2 = -1\\ \bf{q} = \begin{bmatrix} q_w \\ q_x \\ q_y \\ q_z \\ \end{bmatrix} = \begin{bmatrix} q_w \\ \bf{q_v} \\ \end{bmatrix}$$

• Unit Quatornion Properties

  • Relation to angle-axis

    $$w = cos\frac{\theta}{2} q_v = sin\frac{\theta}{2} r$$

  • Not unique

    $$q(\theta, r) = q(-\theta, -r)$$

  • Commutativity

    $$q_1 + q_2 = q_2 + q_1$$

  • Conjugate

    $$\bar{q} = cos\frac{\theta}{2} - sin\frac{\theta}{2} r$$

  • Inverse

    $$q^{-1} = \frac{\bar{q}}{\|q\|} = \bar{q}$$

  • Norm

    $$\|q\| = 1 = \sqrt{\bar{q}q}$$

  • Multiplication

    $$p = (p_0, \mathbf{p})\\ q = (q_0, \mathbf{q})\\ pq = (p_0q_0 - \mathbf{p}^T\mathbf{q}, p_0 \mathbf{q} + q_0 \mathbf{p} + \mathbf{p} \times \mathbf{q})$$

  • Operation on a vector ($q$ is representing rotation matrix $R$)

    $$Rp = q* \begin{bmatrix} 0 \\ p \\ \end{bmatrix} * \bar{q}$$